原因と結果の因果関係を分析する回帰分析についての説明です。回帰分析は数多くの過去のデータを元に、将来の原因から結果を予測するために役立つ分析です。理論がわかればEXCELを活用して簡単に導くことができます。
単回帰分析・重回帰分析とは
回帰分析とは、結果となる数値と要因となる数値の関係を調べて、それぞれの関係を明らかにする統計的手法です。
単回帰分析は1つの目的変数を1つの説明変数で予測する関数であり、重回帰分析は1つの目的変数を複数の説明変数で予測する関数です。
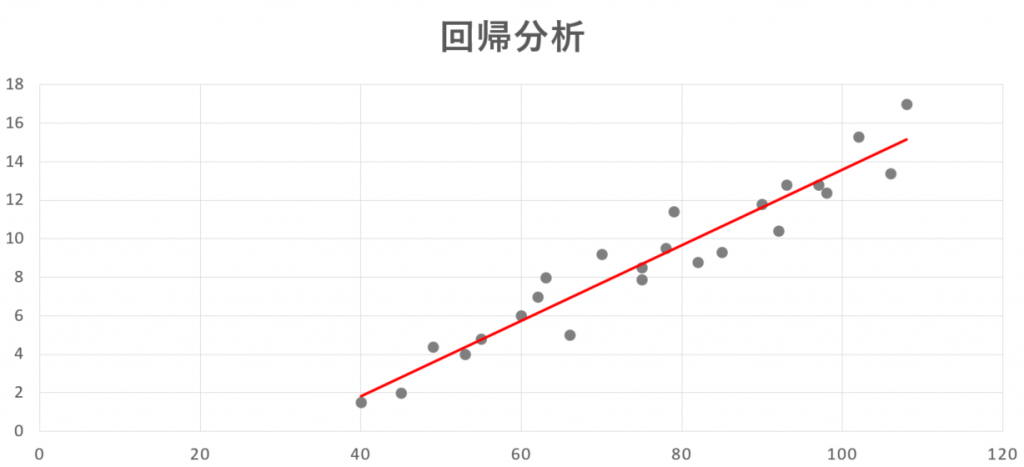
上記のグラフのようにサンプルから単回帰分析の関数を導くことができます。
単回帰分析・重回帰分析の目的
単回帰分析・重回帰分析をマーケティングに活用する目的は、過去のサンプルデータを元にこれから実施するマーケティング施策の成果の見込を立てることです。
例えば、以下のような用途で役立ちます。
- twitterのインプレッション数や番組ページのアクセス数を分析し、テレビ番組視聴率を予測する。
- 曜日・天気・気温を分析し、来店顧客数の予測する。
- ネット広告の配信数からリピート訪問数やオンラインセミナー参加回数を分析して成約数を予測する。
といった具合に、過去のデータを元に将来の予測を導く計算式を求めることができます。
他にも複数の指標にどの程度相関関係があるのかを調べることにも役立ちます。
- 広告施策のコストやSNS運用コストと、売上の相関関係を調べる。
- 価格・品揃え・接客と、売上との相関関係を調べる。
- 築年数、駅からの距離、広さと、不動産価格の相関を調べる。
単回帰分析というと高校数学の確立統計でも習うものです。重回帰分析は大学の学科によって習うものになります。実際の計算は全てツールで行うことができるので、ここでは概略を把握することを目標にしたいと思います。
例えば、原因:広告予算に対して予測される結果:売上と言ったものや、原因:
これから段階的に複雑な話になっていきますが、回帰分析を理解しツールを使いこなすもの大変だと思われた方は、データサイエンティストに相談してもOKです。
単回帰分析と重回帰分析の違い
回帰分析によって、具体的に何ができるか説明します。例えば手元にその日の平均気温とアイスクリームの売上のデータがあったとします。それらのデータを元に、気温(原因)と売上(結果)の相関を導き、どの程度の気温でいくらくらい売上られるか試算することができます。
このように原因となる変数Xが1つ(気温)に対して、結果も変数Yも1つ(売上)の場合の回帰分析を単回帰分析といいます。
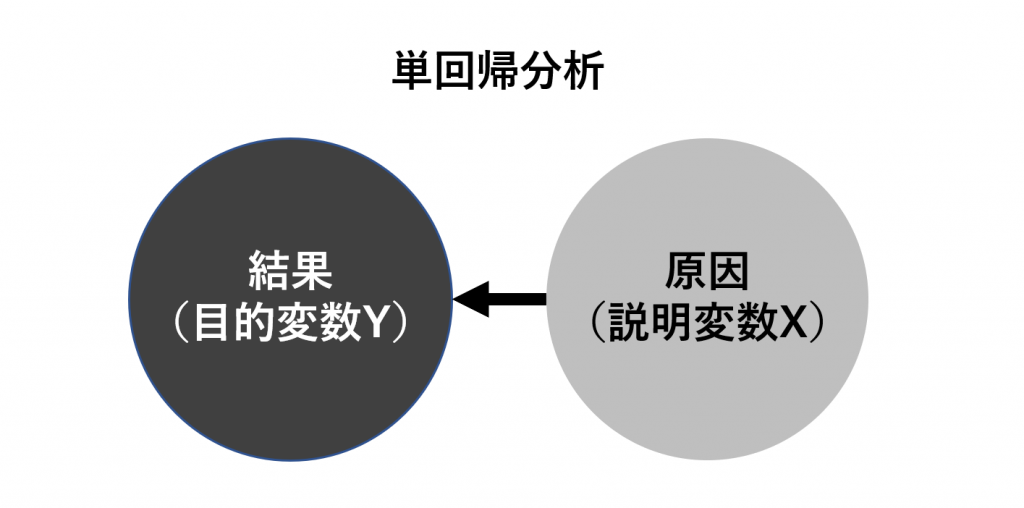
また、アイスクリームの売上に対して、気温と天気の相関関係を調べる場合、原因となる変数Xが2つ(気温と天気)に対して、結果となる変数Yが売上1つ(売上)になります。このように原因となる変数Xが複数ある場合の回帰分析を重回帰分析といいます。
実際のビジネスでは多くの結果は多くの要因によって導かれることが多いため、こちらの重回帰分析の方が使いやすいでしょう。
単回帰分析の説明
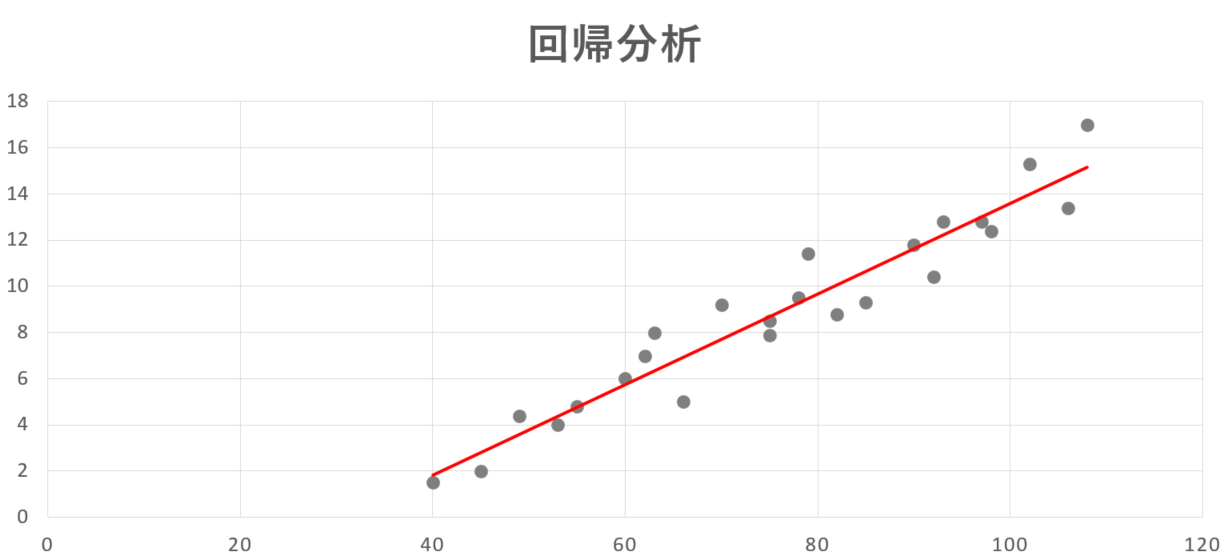
単回帰分析は、結果となる目的変数Yと、原因となる説明変数Xの2軸で構成されるシンプルなものになります。データを以下のような散布図にプロットすることで、各プロットの誤差の最も少ない回帰直線を求めることで単回帰分析を求めることができます。

回帰直線は下記の直線の方程式で表すことができます。
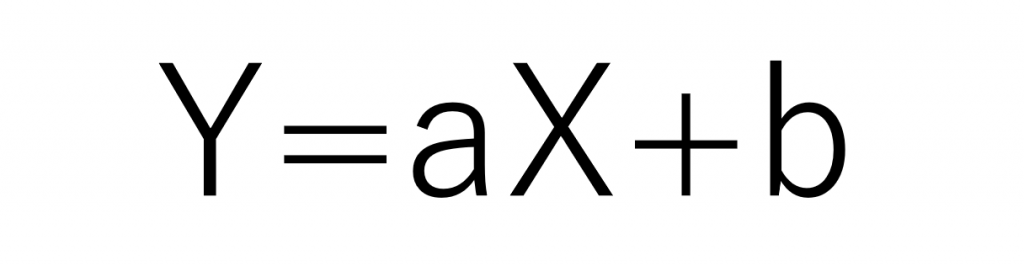
この場合、Yが目的変数、Xが説明変数となります。
重回帰分析の説明
現実のビジネスにおいて結果となる指標Yの要因は、一つだけではなく非常に多岐に及ぶケースが多いので、現実的には単回帰分析よりも、重回帰分析の方がマッチするケースが多いでしょう。
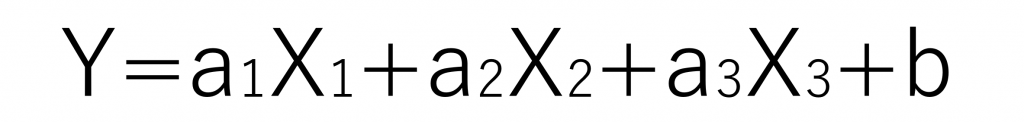
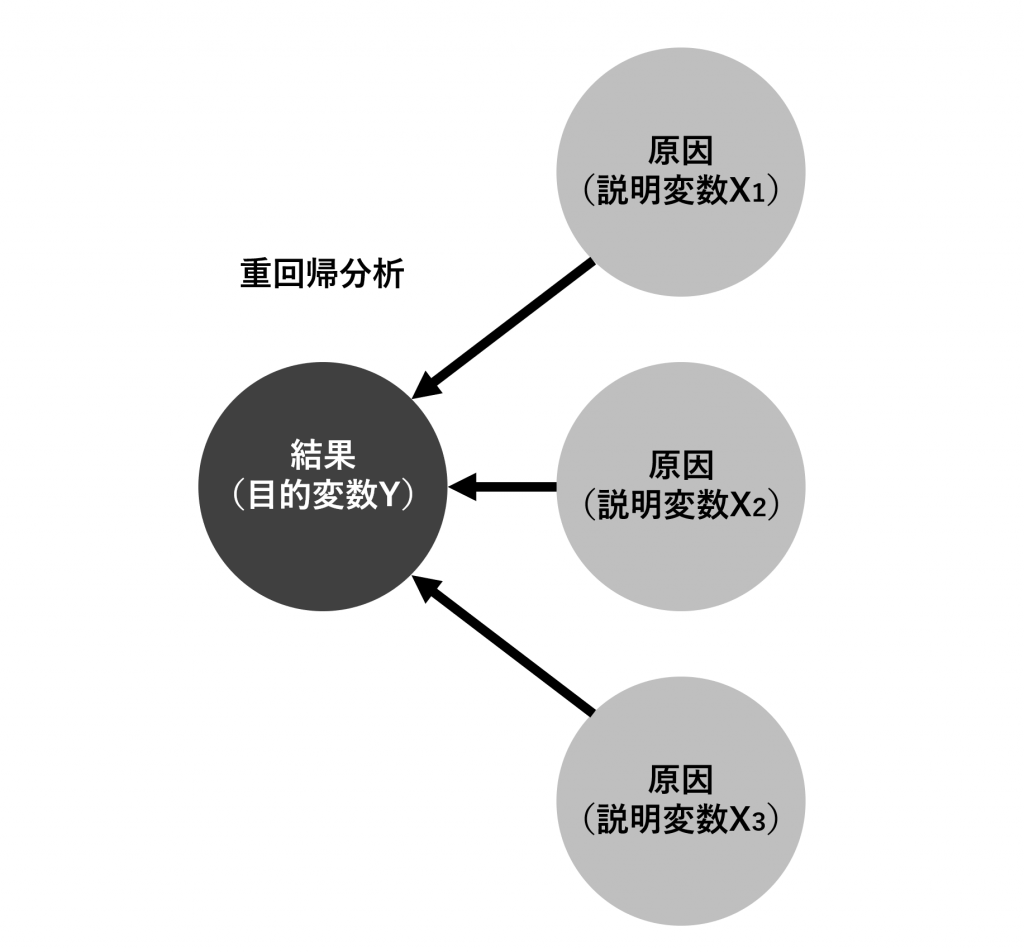
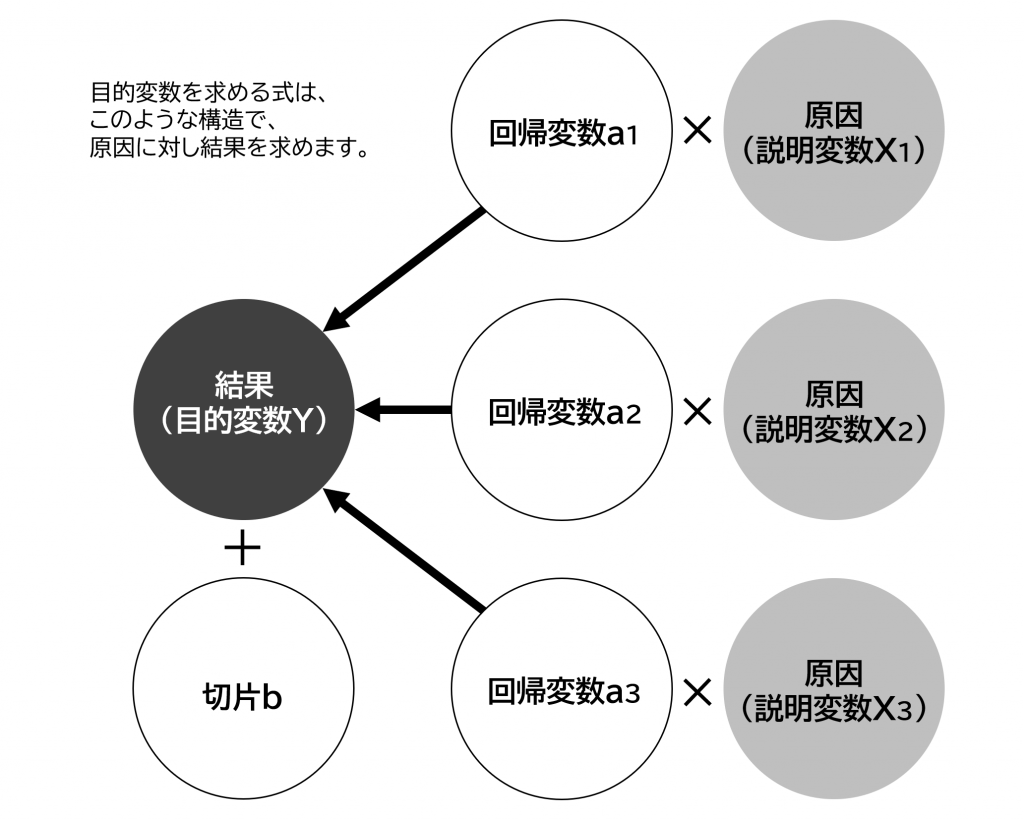
という式で表すことができます。複数の原因となる説明変数X1とX2、X3で、目的変数Yを求めます。
重回帰分析の場合は、このように原因となる説明変数Xが複数あるため2次元のグラフに表すことができません。単回帰分析に比べて、直感的に把握しづらい特徴があります。
回帰分析の注意点・欠点
分析を行う前に、導き出したい結果が重回帰分析で算出できるのかを考える必要があります。 重回帰分析は多変量解析の一つです。多変量解析には主成分分析や判別分析などの分析方法があります。
回帰分析の特徴をしっかり押さえて活用しましょう。
何はともあれデータが必要
過去のデータを元に回帰式を導くことで、今後の予想される説明変数でそもそも過去のデータが豊富にないと十分な分析を行えません。
線形の関係でないと機能しない
この回帰分析の欠点つまり注意すべき点は、回帰分析は基本的に線形性の分析だということです。比例関係にない結果と原因の要素に対して全くの無力といえます。
つまり、相関関係が認められる場合、Xが上がる(下がる)ほど、Yも比例して変化するという前提でないと役に立たないということです。
例えば、結果:「新商品の初月売上」と、原因:「新商品の告知期間」の相関関係をイメージしてみてください。新商品の認知を得るためには一定の時間が必要なので、ある程度発売開始の前から告知をした方がよいといえます。しかし、発売開始の10年前から告知すれば認知が広まり初月売上が上がるかというとそうはなりません。
このように比例関係になりえないものを指標に選んでしまうと期待通りの結果を得ることができません。
指標が線形かどうかを確認する方法
いきなり重回帰分析に取り掛かる前に、結果と原因をひとつづつピックアップして指標を単回帰分析の散布図に回帰直線を引いて目視でチェックしましょう。線形分析が当てはまっていそうであれば、重回帰分析の指標に選ぶと高い精度を期待できます。
多重共線性で精度が下がる
多重共線性とは、相関係数が高い組み合わせがあることをいいます。関連性が強い指標を、説明変数に含めてしまうと精度が下がってしまうのです。たとえば、「身長と座高」といったものです。多重共線性の高い変数を扱い場合は片方を排除します。
曜日や天気などの相関を調べる
気温や降水量と売上の相関などと異なり、曜日や天気などの数値化できないものを分析したい場合は、ダミー変数を使用します。
ダミー変数の例:クーポンありなし
例えばクーポンのありなしで分析したい場合、クーポンありを1、クーポンなしを0と説明変数を定義して分析します。たったこれだけで、あとは通常通り単回帰分析・重回帰分析の手法で分析することができます。
ダミー変数の例:天気
また、ダミー変数の中には天気の様に、晴、曇り、雨、晴れのち曇りなど、2つに区分できないものもあります。その場合は、晴=0or1、曇り=0or1、雨=0or1といった具合に原因となるダミー変数を3つ分けて定義して使います。
ここでやってはいけないのは、晴=0、曇り=1、雨=2といった具合のダミー変数ので意義です。このように定義してしまうと晴、曇り、雨の数値的に厚み付けがなされてしまうため、分析結果の精度を下げてしまいます。注意しましょう。
先の例のクーポンが数種類ある場合は、クーポン種別別に原因変数を増やすことになります。
SNSでのバズなどは対数変換を使う
SNSなどのシェア数などのような、普段は低い数字で推移しているが、ある日突然バズったりして異常に高い数値をたたき出すような数字のばらつきが大きい指標は対数変換を使用することで精度が向上します。
まとめ
以上、単回帰分析、重回帰分析の説明でした。このように統計的に分析する多変量分析の手法は多くあり、目的に応じて使い分けます。これからも目的に応じた分析方法を紹介していければと思います。


コメント