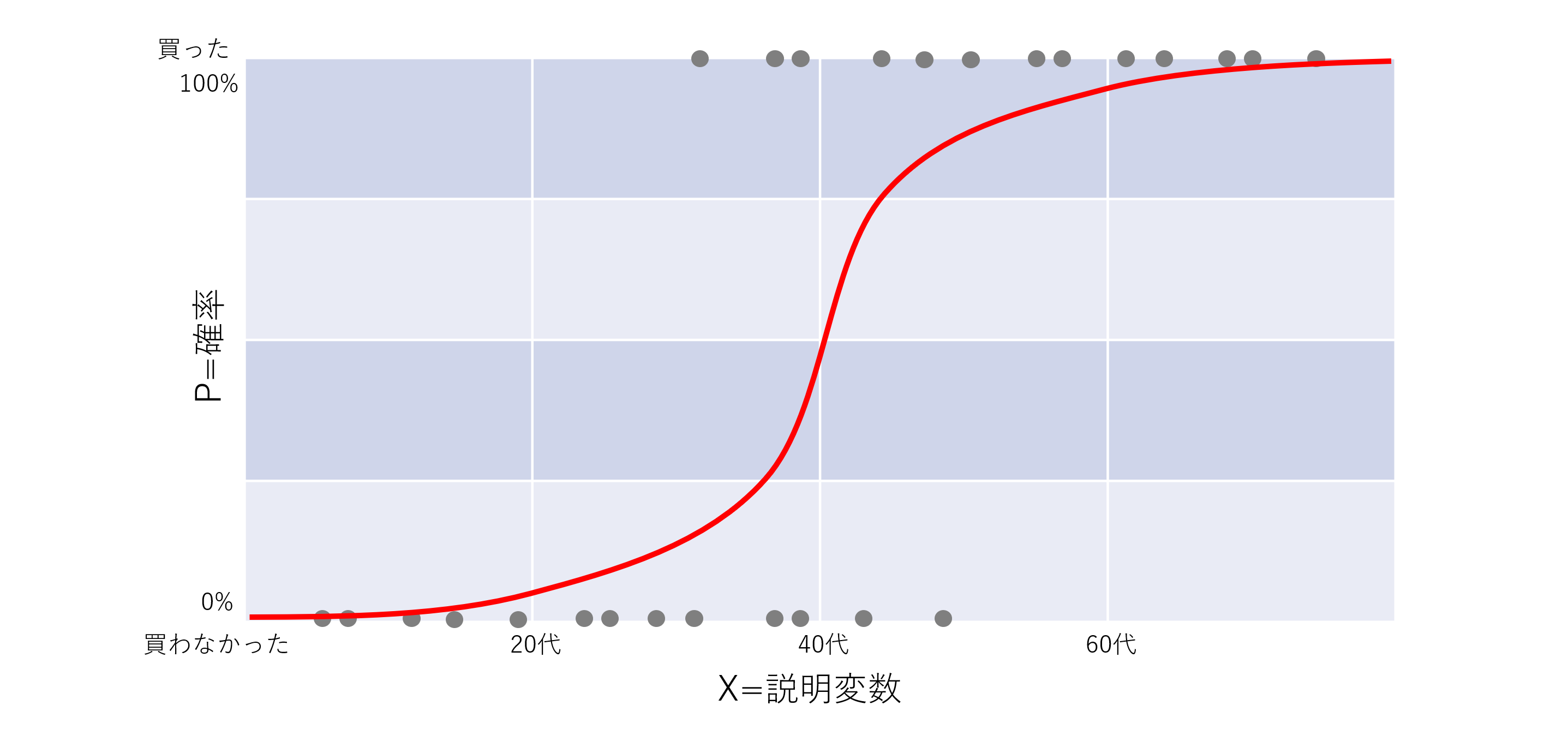
ロジスティック回帰分析とは？マーケティング施策の成果を予測する方法

ロジスティック回帰分析についてです。ロジスティック回帰分析をマーケティングに活用することで、施策を実施する前に結果の予測をすることができます。例えば上記のグラフの例では、年齢によって買ったのか？買わなかったのか？２値の実績データを元に、任意年齢Xの購入率Pを計算する手法です。

ロジスティック回帰分析とは

ロジスティック分析とは、いくつかの要因（説明変数）から発生する確率を説明・予測することができる統計的手法です。

成功するか失敗するか？AかBか？といった２つのうちどちらかの確率を求めることができます。

主にマーケティングで活用する場合、ロジスティック回帰分析の活用目的は、過去のサンプルデータを元に実施するプロモーション施策の結果の確率の見込を実施前に立てることです。

このように、原因は１つではなく複数の原因から、結果の確率を得ることができます。

では、実際の数式を確認してみましょう。実際の計算は全てツールで行うことができるのでご安心ください。また、概略を掴めばあとはデータサイエンティストに発注すればツールを使いこなす必要もありません。ロジスティック回帰分析で何を得ることができるか理解することが大切です。

ちなみに、ロジスティック分析のロジスティックという言葉は物流のロジスティックとは全く関係ありません。

ロジスティック回帰分析は以下のような数式で表します。これによって0か１か結果が分かれる場合1になる確率を求めることができます。

計算式を確認してみましょう。

eは自然対数の底です。これは2.718…とした固定値です。

この目的変数Yを自然対数eのマイナスY乗なので、Yの値が大きければ大きいほど分母は1に近づくわけです。その結果1になる確率は1すなわち100%に近づきます。

Yを表す式は、Y＝目的変数で、Xn＝説明変数となり、重回帰分析で紹介した式と同じ式ですね。

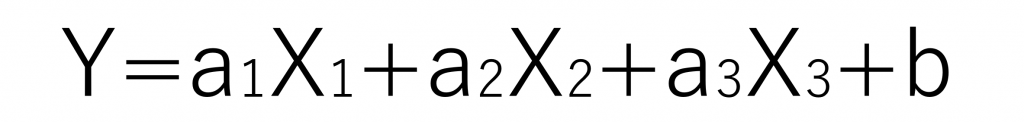
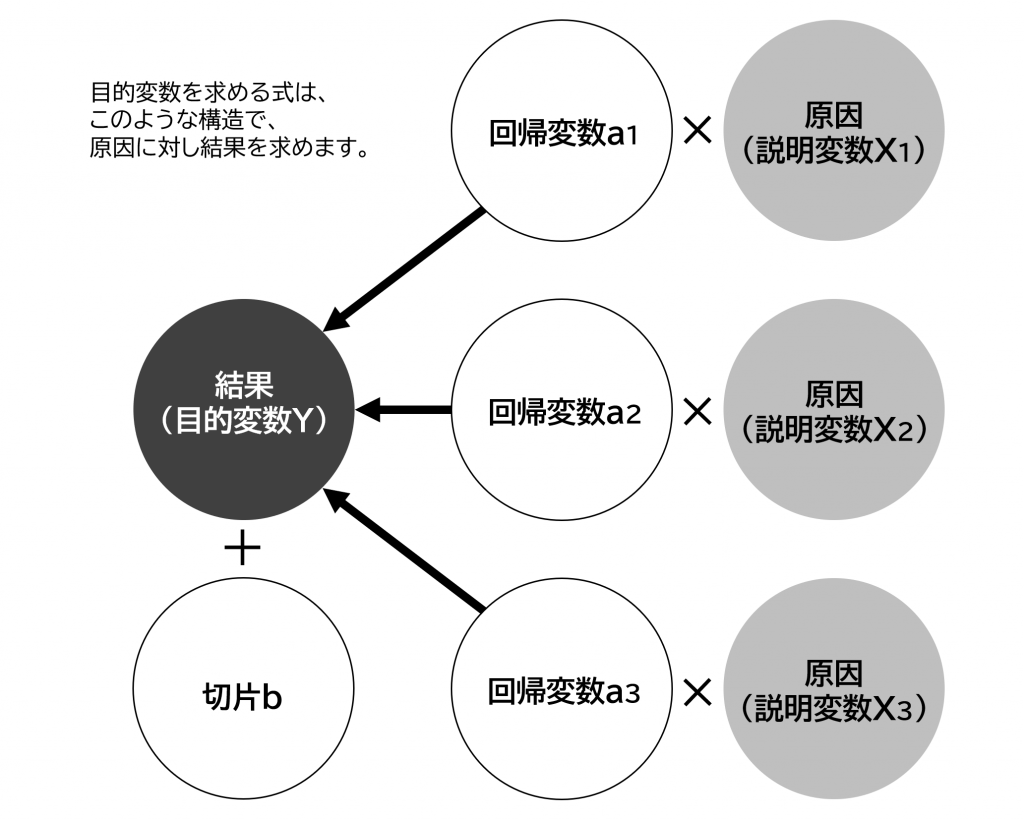
このように線形回帰式と同じような構造を、ロジット変換（オッズを対数化したもの=log(p/1-p) ）することでロジスティック回帰式は出来上がっています。

このように、ロジスティック回帰分析は、単回数分析や重回帰分析に代表される線形回帰分析をレベルアップさせた、一般化線形回帰分析の一つとなります。

ロジスティック回帰分析は、演算した結果は0～1の範囲の確率を求めることができます。つまり、「合格するか？しないか？」「購入するかしないか？」「来店するか？しないか？」「成約するか？しないか？」の２値データの確率を求めることができます。

一方、重回帰分析は、説明変数の結果の値が出てきます。「天気・気温に対し、アイスクリームの販売個数」などといったです。重回帰分析は以下のリンクに詳しく解説しているので是非ご参照ください。

ロジスティック回帰分析では確率ではなく、成功するか否かなどの結果を求めたい場合は、閾値を定めて結果（購入したか購入しなかったかなど）を求めます。

例えば、閾値を0.5（50%）と定めた場合、0.5以上であれば成功、0.5未満であれば失敗といった具合に２値データを求めることになります。

確率から結果を求める閾値は、0.5がそもそも適切なのでしょうか？

設定した閾値の精度を調べる方法についての説明します。適合率（購入すると予測した人のうち実際に購入した人の割合）や再現率（実際に購入した人のうち、購入すると予測で来ていた人の割合）を確認しながら、最適な閾値を求める必要があります。

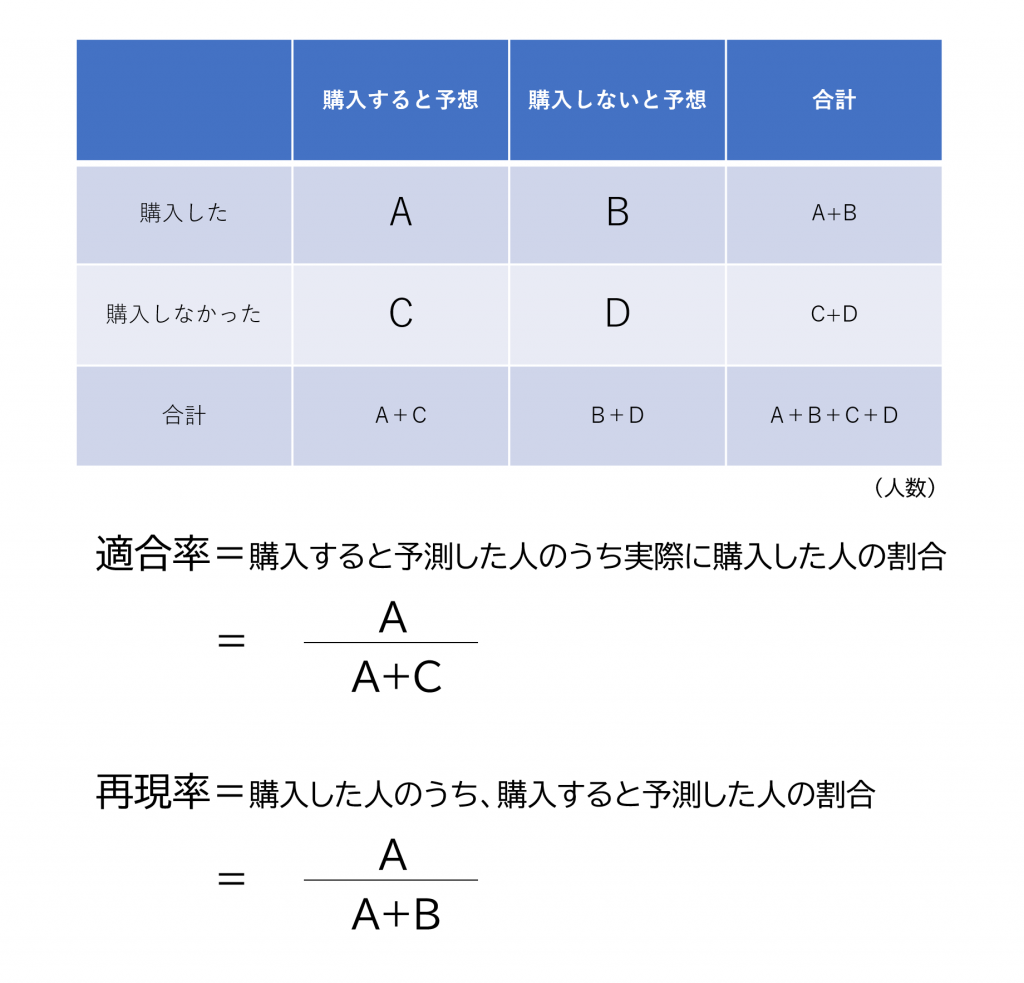
このような指標を用いてロジスティック分析のモデルの精度をチェックし閾値を調整することができます。

オッズとは比率の計測方法の一つです。オッズの場合は、起こらない確率分の起こる確率がオッズとなります。

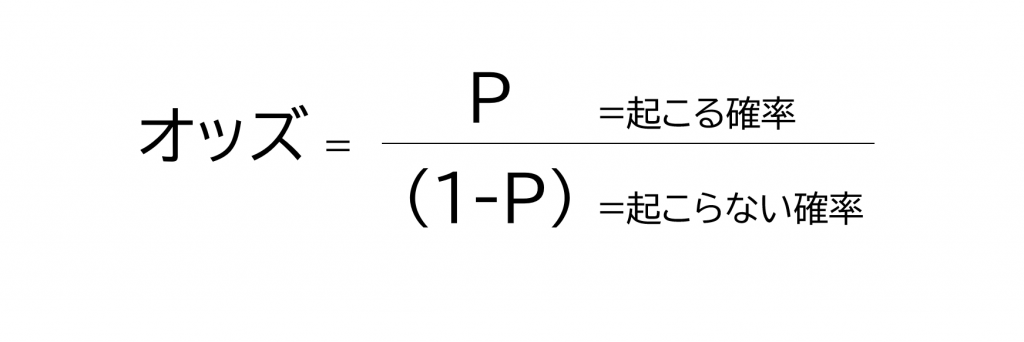
一般的によく使われるいわゆる「割合」は、AとBの割合を計算するときは、全体（A＋B）分のAで算出し、全体に占めるAの割合を使用することが直感的にもわかりやすくなりますが、オッズの場合はB分のAという事になります。

これにより以下のような特徴があります。

オッズは直感的にわかりにくい比率ですが、ロジスティック分析の計算が行いやすいメリットがあるため、よく使用されます。

このオッズを用いたオッズ比で説明変数Xが目的変数Yどの程度影響を及ぼしているか調べます。オッズ比は、オッズ2分のオッズ１で求めます。

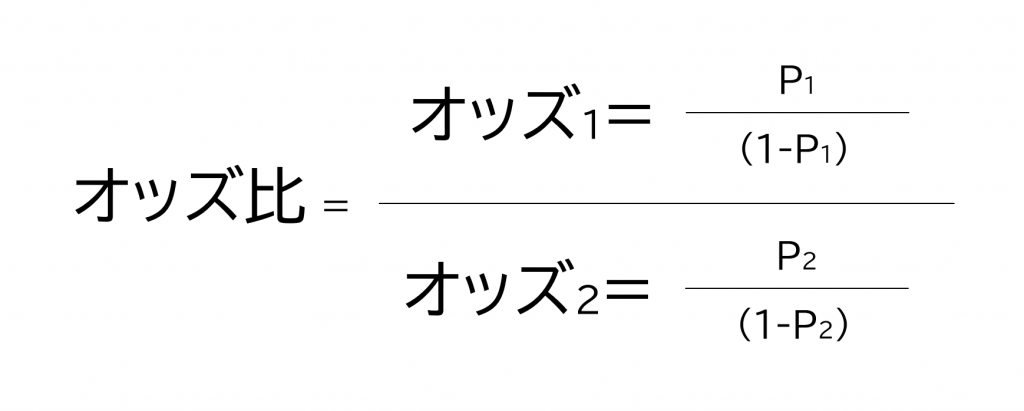
説明変数Xの値を１増やしたときに、どの程度確率値が変わるかオッズ比から変数の影響度を測ることができます。

オッズ比とはXが１増えるとオッズは何倍に増えるのかを表します。オッズ1に対して、説明変数Xが１増やした値をオッズ２と定義します。２つのオッズを比較することでそれぞれの説明変数の影響度を比較することができます。

オッズやオッズ比の読み方については、また改めて記事にしたいと思います。

ではまとめです。

ロジスティック回帰分析は、過去のデータから２値データの確率を求めることができる分析です。
適合率、再現率で精度を図ることができます。
計算式がたくさん出ましたが、計算はできなくても数字の意味だけ分かればツールを使えば自動でやってくれるので十分活用できます。また、ツール使いこなすのも厳しいようであれば、データサイエンティストに発注しましょう。

分析のロジック自体は線形分析と同じモデルなのでシンプルで初期分析に使用するのに優れています。